a. how many rabbits will be on the island one week
after the scientists' arrival?
b. write down a rule for the number of rabbits on the
island n weeks after the arrival of the scientists.
c. how many weeks would it take for this rabbit population
to grow to 600 000?
d. calculate the constant weekly increases that would lead
to a rabbit population of one million on this island, 40 weeks after the scientists'
arrival.
(1995 Further Mathematics CAT3)
Question 2
To help reduce the rabbit population, upon their arrival on the island, the scientists
introduced a viral infection into the rabbit population. The scientists kept a
record of the number of rabbits killed each week by the virus with the following results
for the first three weeks.
| week number |
number of rabbits killed by virus |
| 1 |
512 |
| 2 |
768 |
| 3 |
1152 |
The scientists found that the number of rabbits killed each week by the virus followed
a geometric sequence.
a. Show that the common ratio, r, for this
sequence is 1.5.
b. Calculate the number of rabbits which die from the
virus in week 5.
c. Write down a rule for calculation the number of rabbits
which die from the virus in the nth week of the scientists' stay on the island.
d. Calculate the total number of rabbits which die from
the virus during the first six weeks of the scientists' stay on the island.
(1995 Further Mathematics CAT3)
Question 3
Once the virus had been introduced into the rabbit population on the island, two factors
were affecting the number of rabbits. First, there was a constant increase of 12 000
rabbits per week due to births and deaths by natural causes. Second, there were
additional deaths due to the virus introduced by the scientists.
For the following parts of this question, assume that there was no change in the number of
births and deaths by natural causes, and that the number of deaths due to the virus
followed the geometric sequence as in question 2 above.
a. One of the scientists derived the following equation
for Pn, the size of the rabbit population at the
end of the nth week of their stay (P0
= 360 000).
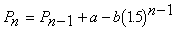
Write down the values of a and b.
b. What will be the rabbit population after the scientists
have been on the island for three weeks?
c. In which week will the rabbit population stop
increasing?
(1995 Further Mathematics CAT3)
Question 4
The following information relates to parts a - c
The Johnstones bought a new car priced at $14 800 and paid a deposit of $1000 each.
They borrowed the balance of the purchase price at simple interest. They then
agreed to repay the loan, plus interest, in equal monthly payments of $442.75 over four
years.
a. Calculate the total amount of interest to be repaid
over the term of this loan.
b. Calculate, to one decimal place, the annual simple
interest rate charged on this loan.
c. The value of this car was depreciated using a reducing
balance method at a rate of 15 percent per year.
i. Calculate, to the nearest dollar, the depreciated value of the car after
three years
ii. Calculate, to two decimal places, the annual percentage rate of depreciation
which would reduce the value of the car from $14 800 to $10 000 in three years.
The following information relates to parts d - f.
The Andersons were offered a $14 800 load to pay the total cost of a similar new car.
Their loan is to be repaid in equal monthly repayments of $500, except for
the last month when less than this will be required to pay out the loan. They will
pay 10.8 percent interest per annum calculated monthly on the reducing balance.
d. Calculate the least number of months needed to repay
this loan plus interest.
e. Calculate the amount of interest, to the nearest cent,
in the final repayment.
f. When the Andersons took out their loan they had the
choice of making monthly repayments of $500 or quarterly payments of $1500. They
chose the make monthly repayments of $500. In either case they would have to pay
10.8 percent interest per annum calculated monthly on the reducing balance. In terms
of the total amount of money they would have to pay to repay the loan, did they make the
correct decision? Explain your answer without making any further calculations.
(1994 Further Mathematics CAT3)
Question 5 (See also Q6,Q7,Q8)
In July 1996, Kelly received the following statement from her bank showing all the
transactions for her savings account for the financial year 1995-96. The financial
year begins 1 July 1995 and ends 30 June 1996.
| date |
transaction detail |
debit |
credit |
balance |
| 01 Jul 1995 |
balance forward |
|
|
1 650.00 |
| 01 Jul 1995 |
interest |
|
50.00 |
1 700.00 |
| 01 Jul 1995 |
withdrawal |
150.00 |
|
1 550.00 |
| 23 Sep 1995 |
deposit |
|
2 350.00 |
3 900.00 |
| 15 June 1996 |
withdrawal |
|
|
3 120.00 |
a. In the space provided in the table above, write down
the amount of the withdrawal made by Kelly on 15 June 1996.
b. Interest at a rate of 6 percent per annum is
paid. What is the monthly interest rate?
c. Interest is paid on 1 July each year. It is
calculated monthly and based on the minimum monthly balance. How much interest was
earned for the month of October 1995?
d. How much interest would be paid into Kelly's account on
1 July 1996?
(1996 Further Mathematics CAT3)
Question 6 (See also Q5,Q7,Q8)
Kelly is saving money to put towards the purchase of a new car. She has had
her present car for five years and it cost her $12500. To know how much money she
will need to borrow she must estimate the current value of her present car.
a. What will be her estimate of the current value of her
car if she assumes that it has depreciated at a flat rate of 12 percent per annum?
b. What will be her estimate of the current value of her
car if she assumes that it has depreciated at a rate of 16 percent per annum on its
reducing value? Give your answer to the nearest one hundred dollars.
(1996 Further Mathematics CAT3)
Question 7 (See also Q5,Q6,Q8)
On 1 July 1996, Kelly trades her old car in for $6500 on a car worth $15 400. To
repay what she sill owes, Kelly considered two options:
option 1: borrowing all the money owed
option 2: using part of her savings to reduce the amount she would have to borrow
a. Following option 1, Kelly can obtain a reducing balance
loan to be paid off over three years. In this time she would repay a total of $11
712.35. How much of this amount is interest?
b. Following option 2, Kelly could withdraw $3000 from her
savings account and use it with her trade-in to reduce the amount of money she would have
to borrow.
i. How much would she now have to borrow?
ii. Use the annuities formula to calculate, to the nearest cent, the
quarterly repayment that would enable this loan to be paid off in three years at a
quarterly interest rate of 4.5 percent.
iii. Calculate the total amount of interest paid in repaying this loan.
(1996 Further Mathematics CAT3)
Question 8 (See also Q5,Q6,Q7)
Kelly wants to compare the two options for financing her car as set out in
Question 7.
a. Calculate the interest saved over the three-year period
if option 2 is abopted. Ignore any interest she would have earned on the $3000 she
would have withdrawn from her savings account.
b. Calculate the interest savings over the three-year
period if option 2 is abopted but now take into account the interest Kelly would have
earned by leaving her $3000 in her savings account. Interest is paid at a rate of 6
percent per annum compounding.
(1996 Further Mathematics CAT3)
Copyright Information:
This material is an extract of material produced by the Board of
Studies, Victoria, Australia. This material is copyright and cannot be reproduced in any
form without the written permission of the Board of Studies.
Visit Board of Studies Website for more
information on VCE.
