| activity |
description |
predecessor |
duration (days) |
| A |
build foundation |
- |
5 |
| B |
build frame |
A |
8 |
| C |
build roof |
B |
12 |
| D |
do electrical wiring |
B |
5 |
| E |
put in windows |
B |
4 |
| F |
install insulation |
E |
1 |
| G |
install plumbing |
F |
1 |
| H |
put on siding |
G |
6 |
| I |
paint house |
C,H |
3 |
| J |
add fixtures/fittings |
D,I |
3 |
A project network for this plan, with activities on arcs, is given in Figure 1 below.
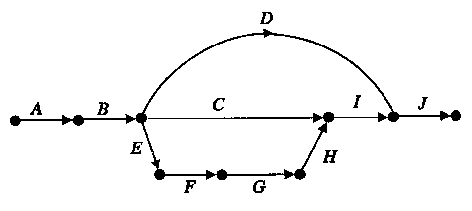
Figure 1
Question 1
Using the information in Table 1 determine and write in the times missing from table 2
Table 2
| activity |
earliest start time |
latest time table |
| A |
0 |
0 |
| B |
5 |
5 |
| C |
13 |
13 |
| D |
13 |
|
| E |
|
13 |
| F |
17 |
|
| G |
18 |
18 |
| H |
19 |
19 |
| I |
25 |
25 |
| J |
28 |
28 |
(1995 Further Mathematics CAT3)
Question 2
What is the earliest time in which the project can be completed using the information
given in Table 1?
(1995 Further Mathematics CAT3)
Question 3
What is/are the critical path/paths in this network?
(1995 Further Mathematics CAT3)
Question 4
What is the float (slack time) for any activity not on a critical path?
Like many construction projects this can have its time reduced by 'crashing' the project,
that is, using more resources to finish parts of the job more quickly. Table 3 gives
the cost of these reduction and the maximum extent to which each action can be taken.
Table 3
| activity |
cost per day for reducing activity duration ($) |
maximum possible reduction (days) |
| A |
300 |
2 |
| B |
150 |
3 |
| C |
200 |
1 |
| D |
400 |
2 |
| E |
200 |
2 |
| H |
300 |
3 |
| I |
400 |
1 |
| J |
150 |
1 |
Question 5
a. Using the information in Table 3, determine the
shortest time in which the project can now be completed. Show all working.
b. What is the minimum additional cost to achieve this?
show all working
(1999 Further Mathematics CAT3)
Question 6
Jack's company is building the new Bigtown University. The company has constructed
nine new faculty buildings in a layout as shown in Figure 2. The minimum distances
in metres between adjacent buildings in the university are also shown.
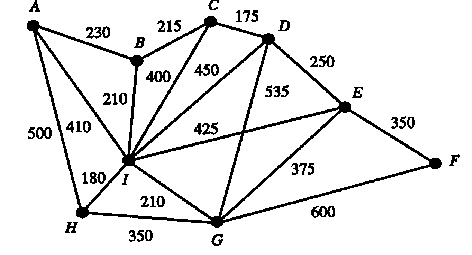
A computer network is to be built to serve the whole university.
a. Draw a network which will ensure that all the buildings
are connected to the network but which also minimises the amount of cable used.
Label each node in the network.
b. What is the minimum length of cable required?
(1999 Further Mathematics CAT3)
Question 7
In another project, Jack has four jobs to be done on the same day and four workers, Tara,
Joe, Adam and Kate, available to work on that day. Not all jobs can be done by each
of the workers. Tara and Joe can each do job A, Adam can do job B or C and Kate can
do job C or D. Each worker can do only one job on that day. The possible
allocation of the workers to the project can be represented on a network flow diagram as
shown in Figure 3
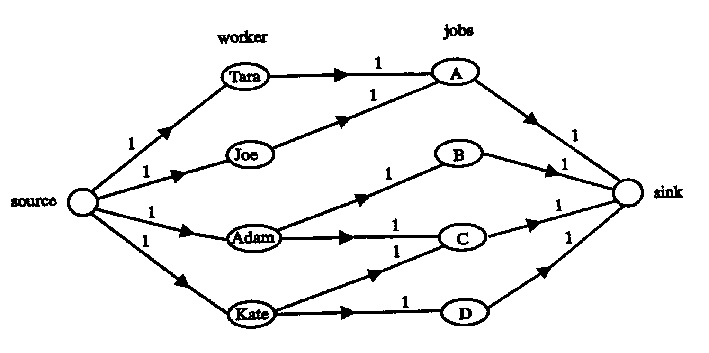
Figure 3
Using the diagram to determine the maximum flow and use this information to see if the
project can be completed with the workers available. Clearly show each step of your
working
(1999 Further Mathematics CAT3)
Copyright Information:
This material is an extract of material produced by the Board of
Studies, Victoria, Australia. This material is copyright and cannot be reproduced in any
form without the written permission of the Board of Studies.
Visit Board of Studies Website for more
information on VCE.
