We hear and make statements that involve probability all the time.
For example:
It will probably rain tomorrow
I am certain that the sun will rise tomorrow morning.
The South African cricket team is the favourite to win the world cup.
Probability involves making predictions about things that may or may not happen.
Probability is used by scientists, economists, gamblers etc.
Terms used in the study of probability
Experiment: The work or
activity that generates the results to be studied.
Outcome: The result of an
experiment.
For example:
| Experiment |
Outcome |
| Toss a coin |
{head, tail} |
| Roll a die |
{1,2,3,4,5,6} |
| Football game |
{win, lose, draw} |
Sample space or Outcome space: All possible
outcomes.For example,when a die is rolled the sample space will be {1,2,3,4,5,6},and
sample space is usually denoted by the symbol S.
S = {1,2,3,4,5,6 }, n(s) = number of outcomes = 6
Event: A collection of
outcomes from a specified sample space.For example when we rolled a die,we could define an
event A as odd numbers
A = {1,3,5 }, n(A) =
number of outcomes = 3
Pr(Event): The probability
of an event occuring.

Probabilities can be expressed as a fraction, as a decimal, or as
a percentage.
In the above example, if we want to calculate the probability of getting an odd number,
S = {1,2,3,4,5,6 }
Total number of possible outcomes, n(S) = 6
A = { 1,3,5 }
Number of successful outcomes, n(A) = 3

The terms we use to describe the
chances.
Impossible : Impossible events have probabilities of
zero.
Unlikely : Very
unlikely events have probabilities close to zero.
Even chance : Even chance events have
probabilities close to 0.5
Likely
: Very likely
events have probabilities close to one.
Certain : Certain
events have probabilities of one.
The complement: The
complement of an event is the event which does not happen. For example the complement of
success is failure and the compliment of failure is success. If the event is A,
the complement of A is written as A' .
If I rolled a six sided die, what is the probability of
:
(a) getting a 6
(b) not getting a 6
S = { 1,2,3,4,5,6 } these are the possible outcomes.
Number of possible outcomes, n(S) = 6
A = getting a 6, number of successful outcomes n(A) = 1
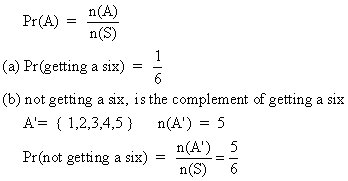
The outcomes for tossing a coin are {Head (H), Tail (T)
}
The outcomes for rolling a die are { 1,2,3,4,5,6 }
The possible outcomes for the combined event are:
{H1, H2, H3, H4, H5, H6, T1, T2, T3, T4, T5, T6}
There are 12 possible outcomes.
We can use a tree diagram
to list the sample space.

We can use a lattice diagram
to show the sample space.

Head
|
H
|
(1,H) |
(2,H) |
(3,H) |
(4,H) |
(5,H) |
(6,H) |
 Tail Tail
|
T |
(1,T) |
(2,T) |
(3,T) |
(4,T) |
(5,T) |
(6,T) |
|
1
 |
2
 |
3
 |
4
 |
5
 |
6
 |
| Rolling a die |