| Addition of Directed Numbers Let's
consider -3 + + 4
In this problem + and + signs are side by side.There is no number in between
them. So the two positive signs which are side by side gives a positive sign.
Remember this,
Two like signs give a positive sign
+ + = +
-3 + + 4 = - 3 + 4
= 1
Sometimes directed numbers are written as
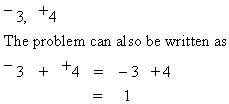
Let's
consider - 3 + - 4
In this problem positive (+) and negative (-) signs are side by side without a
number in between them. Two unlike signs which are side by side gives a negative (-) sign.
Remember this:
Two unlike signs give a negative sign.
+ - = -
-3 + - 4 = -3 - 4
= - 7
Subtraction of Directed Numbers
Let's consider -3 - - 4
In this problem the middle negative(-ve) signs are side by side without a number
in between them. So the like signs which are side by side, always give a positive sign.
-3 - - 4 = -3 + 4 =
1
This problem can also be written as
-3 -(- 4) = -3 + 4
= 1
and
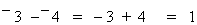
Let's consider -3 - + 4
In this problem negative(-ve) and positive(+ve) signs are side by side without a
number in between them.
That is two unlike signs are side by side, which gives a negative(-ve) sign.
-3 - + 4 = -3 - 4
= - 7
This problem can also be written as
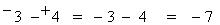
and
-3 - (+ 4) = -3 - 4
= -7
Multiplication of Directed Numbers
Let's consider -3 × -4
When multiplying directed numbers
Two like signs always give a
positive(+ve) sign
Two unlike signs always give a
negative(-ve) sign
(-ve) ×
(-ve) =
(+ve)
-3 × -4 =
12
-3 × +4 =
-12
(-ve) × (+ve)
= (-ve)
Dividing directed numbers
When dividing directed numbers
Two like signs always give a
positive(+ve) sign
Two unlike signs always give a
negative(-ve) sign
Let's consider -3 ÷ -4
Two like signs give a positive sign
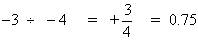
Let's look at this problem.
-8 + (6 × -3 - 2) ÷ -4 - -8
In this problem you can see all different operations, when we have more than one
operation we have to follow the order of operations.
ie. 1. Brackets
2. Division or multiplication from
left to right
3. Addition or subtraction from left
to right
Let's do the brackets first (6 × -3 - 2), inside this bracket you
can see the multiplication and the subtraction signs. Remember the order, we have to do
multiplication first and then the subtraction
O.K 6 × -3
= - 18 (multiplying two unlike signs,gives a negative
sign.)
Then we
subtract 2
(6
× -3 - 2) = -18 -2 = -20
Now our problem
-8 + (6 × -3 - 2) ÷ -4 - -8 = -8 + (-20) ÷ -4 -
-8
What's next?, addition,subtraction or division.
Remember the order, division comes before addition and subtraction.
O.K (-20) ÷ -4 = +5 (dividing
two like signs, gives a positive sign.)
Now our problem
-8 + (6 × -3 - 2) ÷ -4 - -8
= -8 + (-20) ÷ -4 - -8
= -8 + +5 - -8(two like signs without a number in between them gives a
positive sign)
= -8 + 5 + 8 now we are left with only addition and
subtraction signs,so we can work out this problem from left to right.
= -3 + 8
= 5
|