[Home][General][Business][Engineering][VCE][Learning Units][Tool Box][Glossary]

Back to Graphs Units

Linear relationships are used in everyday life.These relationships can be expressed in many different ways. Linear graphs are one way of expressing these relationships, when graphed they give a straight line. Linear graphs can be sketched or plotted. Plotting a Straight Line Graph Sketching a Straight Line Graph Key Facts about Graphs Gradient between two points         Plotting a straight line graph: Use  graph paper or grid paper for accuracy. Use X and Y as variables. Give values to X and work out the values of Y, set these values in a table. Place the axes in the most suitable position, to give the best presentation of the graph. Choose a suitable scale. Plot the points from your table of values. Join the points to give a straight line.     Sketching a straight line graph: Graph paper or grid paper are not necessary. Only two points are necessary to sketch a straight line graph. Join the two points to give a straight line.   There are different ways of writing   a linear equation or an equation of a straight line. y = mx + c , where m is the gradient and c is the y-intercept. ax + by + c = 0, where a, b, c are constants. y-y1 = m (x - x1), where m is the gradient and x1 and y1 are co-ordinates of a given point. If you are not sure about the terms, go to Graphs- basic terms.       Key facts about the gradients and the shape of the straight line graphs:       .

 

 

 

 

 

 

 

Examples

 

 

Example 1: Draw the graph of the linear equation  y = 2x +3

Example 2: Sketch the linear equation y = 2x +3 , using the x- and y- intercepts.

Example 3: Rearrange the linear equation,  3y + 4x = 12   to  y= mx + c   form and find the y- intercept .

 

 

 

 

 

 

 

Example 1. Draw the graph of the linear equation  y = 2x +3 First make a table. Let's choose x values between -3 and +3 row1 x -3 -2 -1 0 1 2 3 (1) 2�row1 2x -6 -4 -2 0 2 4 6 (2) add 3 +3 +3 +3 +3 +3 +3 +3 +3 (1)+(2),  y = 2x+3 -3 -1   1   3   5   7   9 Plot these points on a number plane as shown below. Return to Examples   Return to Examples     Example 2. Sketch the linear equation y = 2x +3 , using the x- and y- intercepts.    To find the x-intercept, let y =0    When y =0,   2x + 3 = 0                                2x = -3                                 x = -3 � 2 = -1.5    Now we can write the co-ordinates of the x-intercept as (-1.5,0)   To find the y- intercept, let x =0   When x = 0, y = 2�0 +3                       y = 3 Now we can write the co-ordinates of the y-intercept as (0,3) Return to Examples We can join  (-1.5,0) and (0,3) to sketch the graph.   Return to Examples         Example 3. Rearrange the linear equation,  3y + 4x = 12   to  y= mx + c   form and find the y- intercept . 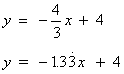3y+4x =12 3y    = -4x + 12   y  = (-4x +12) � 3   y  = (-4x � 3)  +(12 � 3) Return to Examples     Leave the y term on the left hand side(L.H.S), and take all the other terms to the   right hand side(R.H.S.), now you have 3y = -4x +12 Then divide the whole equation by 3 to give y by itself. Now you have rearrange the equation to y = mx + c form. So the gradient is m = -1.33 y-intercept , which is c =4

 

 

 

 

 

 

Have a Go Problem 1 Find the gradient between A(2,5) and B(4,9) and then find the equation of the straight line.     Problem 2 Find the X- and Y intercepts for y =5x -3 and hence sketch the graph.

 

 

 

 

 

 

Practice Questions Question 1 Find the gradient between A(1,-4) and B(-1,4)   Answer m = - 4 Question 2 State the gradient and y-intercept of 2y = 6 x - 8   answer m=3, y intercept (0, -4)   Question 3 Find the gradient between A(4,2) and B(-3,2) and hence find the equation of line AB.   answer m=0, y=2   Question 4 Sketch  3y = -6 x +15 click here to check your answer

 

 

 

 

 

 

Solution 1 Find the gradient between A(2,5) and B(4,9) and then find the equation of the straight line. Let A(2,5) =(x1,y1) and B(4,9) =(x2,y2) m = 2 and  (x1,y1) =(2,5) Equation of the straight line is: back to Have a Go                  y -  y1 = m(x - x1)                           y - 5   = 2 (x - 2)                   y - 5  = 2x -4                      y     = 2x -4 +5  (add 5 to both sides, on L.H.S. -5 +5=0)                      y    =  2x + 1

Solution 2 Find the X- and Y intercepts for y =5x -3 and hence sketch the graph.   To find the x-intercept, let y =0    When y =0,   5x -3 = 0                                5x = 3                                 x = 3 � 5 = 0.6    Now we can write the co-ordinates of the x-intercept as (0.6,0)   To find the y- intercept, let x =0   When x = 0, y = 5�0 -3                       y = -3   Now we can write the co-ordinates of the y-intercept as (0,-3) We can join the points (0.6,0) and (0,-3) to sketch the graph.   back to Have a Go

 

                                       

 

Answer to Practice Question 4

 

[Home][General][Business][Engineering][VCE][Learning Units][Tool Box][Glossary]