[Home][General][Business][Engineering][VCE][Learning Units][Tool Box][Glossary]

Back to Algebra Units   Rule1: Do the same thing When working with equations remember to do the same thing to both sides of the equation.   Rule2: Choose Oppsite Operation To transpose something do the oppsite operation on it when carrying it across the equal sign.

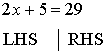
Transposition is a skill you need to learn to solve most algebra equations. All equations have two sides- a Left Hand Side (LHS) and a Right Hand Side (RHS).  For example in the equation below 2x + 5 is on the Left Hand Side of the equation and 29 is on the Right Hand Side of the equation: There are many ways to solve transposition problems. One way is to do the same thing to both sides of the equation with the aim of bringing like terms together and isolating the unknown quantity. So, to solve this equation, first subract 5 from both sides of the equation. 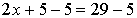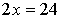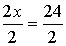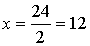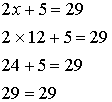This action will get rid of number 5 from the LHS which simplifies to: Now, 2x equals to 24, so if we divide both sides with 2, we can get the value of x that is: Check Your answer: Now, if your answer for x is 12, you can substitute this value in the original equation to check if your answer is correct: So, your answer x=12 is correct.

 

 

Examples

Example 1: x+ 3  = 8 x + 3 - 3 = 8 - 3 x = 8 - 3 x = 5 Comment: Since 3 is with a + sign on the LHS, we subtract 3 from both sides. A +3 and a -3 cancel each other on the LHS. Check Answer: x + 3 = 8 5 + 3 = 8 Example 2: x - 5  = 2 x - 5 + 5 = 2 + 5 x = 2 + 5 x = 7 Comment: Since 5 is with a - sign on the LHS, we add 5 to both sides. A -5 and a +5 cancel each other on the LHS. Check Answer: x - 5 = 2 7 - 5 = 2 Example 3: 3x = 15 x = 5 Comment: Since 3 is multiplying x on the LHS, we divide both sides by 3. On the LHS 3x divided by 3 gives us x. Check Answer: 3x = 15 3 x 5 = 15 Example 4: x = 18 X 3 x = 54 Comment: Since 3 is dividing x on the LHS, we multiply both sides by 3. So on the LHS 3 divided by 3 is cancelled out leaving x. Check Answer: Example 5: 2x + 5 = 35 - 4x 2x + 4x + 5 = 35 - 4x + 4x 6x + 5 = 35 6x + 5 - 5 = 35 - 5 6x = 30 x = 5   Since there is a -4x on the RHS we add a +4x on both sides. On the RHS -4x and +4x cancel each other out. Since there is a +5 on the LHS we subtract 5 from both sides. On the LHS +5 and -5 cancel each other out. Since 6 multiplies x on the LHS we divide both sides with 6. On the LHS 6 divided by 6 cacel each other leaving x. Check Answer: 2x + 5 = 35 - 4x 2x5 + 5 = 35 - 4 x 5 10 + 5 = 35 - 20 15 = 15 Example 6: multiply each term by 20 to remove fractions 13x + 17 = 40 13x + 17 - 17 = 40 - 17   This equation involves fractions and we should try to get rid of fractions first. We do this by multiplying each term with 20 (lowest common factor for 5 and 4 is 20)     5 cancels out 20 by 4 in the first term and 4 cancels out 20 by 5 in the second term leaving 4(2x+3) + 5(x+1)=40 Collecting like terms togther we get 13x+17=40 since there is a +17 on the LHS, we subtract 17 from both sides. On the LHS the +17 cancels out -17. Since 13 multiplies x on the LHS we divide both sides by 13. On LHS 13 divided by 13 cacel each other out. Leaving x equal to 23 divided by 13. Check Answer: Here we'll do a simple check using estimating techniques. x is 23/13 which is nearly 2, so if we substitute 2 for x in the equation we can evaluate the LHS of the equation to be about 2 suggesting your answer is probably correct.

 

 

 

 

 

Have a Go Solve the following for x 1.  2x + 2 = 1 2. 3x - 5 = 7 3. 7 - x = 2       Solve the following for y 1.  8y - 7 = 2y + 5 2. 3.

 

 

 

 

 

 

Practice Questions Question 1 Solve for y: 2y - 5 = 3 Answer y=4 Question 2 Solve for x: 2(x + 4) = 23 answer x=7.5 Question 3 Solve for x: 2x + 5 = x + 6   answer x=1 Question 4 Solve for k: 6(k - 3) = 0   answer k=3 Question 5 Solve for m:   answer m=-7   Question 6 Solve for x:   answer x=1/3

 

 

 

 

Solution Problem1 2x + 2 = 1 2x + 2 - 2 = 1 - 2 2x = -1 Problem 2 3x - 5 = 7 3x - 5 + 5 = 7 + 5 3x = 12 x = 4 Problem 3 7 - x = 2 7 - 7 -x = 2 - 7 -x = -5 x = 5 Back to Have a Go

Solution Problem1 8y - 7 = 2y + 5 8y - 2y = 5 + 7 6y = 12 y = 2   Problem 2 multiply all terms by 30 y = 15 Problem 3 multiply all terms by 12 Back to Have a Go

 

[Home][General][Business][Engineering][VCE][Learning Units][Tool Box][Glossary]